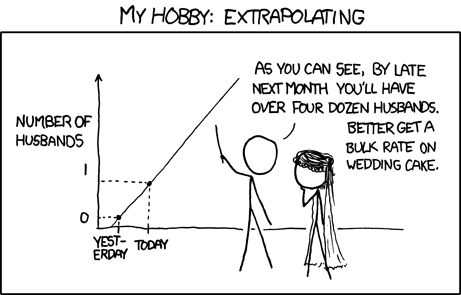
Original post is not linearly interpolating but exponentially.
this comic uses a log scale (I extrapolate this from the only two data points given).
(apologies for pedantry) This can’t be the case, as the zero point is visible in the graph and even gets crossed to the negatives. Log scale graphs only show positive values and place zero infinitely below the horizontal axis.
If that were the case, the y-axis label would be
log(NUMBER OF HUSBANDS), no?It’s a choice, it’s not mandatory to use a log on your y axis when you plot a log.
Nice. Haven’t thought about that 🤣
New data point in 3…2…
Neatly showing why when all you have is two data points you can’t just assume the best fit function for extrapolation is a linear one.
Mind you, a surprisingly large number of political comments is anchored in exactly that logic.
Doubling every three months is an exponential interpolation and not a linear one!
Good point and well spotted!
PS: Though it’s not actually called exponential (as it isn’t enr-3-month-periods but rather 2nr-3-month-periods ) but has a different name which I can’t recall anymore.
PPS: Found it - it’s a “geometric progression”.
By tweaking a few parameters you can turn every base into any other base for exponentials. Just use e^(ln(b)*x)
PS: The formula here would be e^(ln(2)/3*X) and x is the number of months. So the behavior it’s exponential in nature.
By that definition you can turn any linear function a * x + b, “exponential” by making it e^ln(a*x +b) even though it’s actually linear (you can do it to anything, including sin() or even ln() itself, which would make per that definition the inverse of exponential “exponential”).
Essentially you’re just doing f(f-1(g(x))) and then saying “f(m) is em so if I make m = ln(g(x)) then g(x) is exponential”
Also the correct formula in your example would be e^(ln(2)*X/3) since the original formula if X denotes months is 2X/3
It doesn’t matter if you divide ln(2) or x by three, it’s the same thing.
Get a room you two
PPS: Found it - it’s a “geometric progression”.
A terminology that I learned from the Terminator 2 movie. Only that was, I think, a “geometric rate”.
Chessboard and wheat
One of the best mathematical stories from ancient times, IMHO,
It’s cold today, so much for climate change 🧐
Close, if you’d instead called it global warming I’d have bought it
Dammit, we’re on a cooling trajectory, prepare for a new ice age and the approach to absolute zero by end of year
Huge if true!
If you’ve ever seen a growth chart, you know that newborns grow incredibly quickly, but the rate of growth tapers off over time. That being said, my daughter will be six feet tall by the time she’s 2:

It looks like he aged 5 years in 3 months…
Someone’s clearly not a parent.
Oh oh, don’t tell me, I’ll guess! It’s the baby, right? The baby’s not a parent?
You are correct
Babies grow super fast.
I was talking about the dad, lol.
I should have been more specific given they are both male.
Oh, yeah. That makes a lot more sense! And that’s what being kept up every night for months will do to you.
To be fair, the lighting conditions are way more flattering in the first pic. When you have even lighting all over your front, it minimizes wrinkles. The second pic seems like it was taken in the evening with only one light source (or a few…but it seems like maybe an overhead porch light), making wrinkles and such far more prominent.
As a parent with a kid who didn’t sleep well I knew what you meant lol
As a father I can confirm this seems right
Why is the wreath still there?
3 months of chronic sleep deprivation
How’re the kids?
Do we tell him?
It’s not his?
That’s Maury’s job, not ours.
That it’s not Christmas anymore?
There’s another problem that his math missed. His baby-making rate stands at one per three months. Extrapolating that for all humans puts the population’s doubling rate at EVERY THREE MONTHS! In 10 years, there will be a lot of ~3 trillion kg kids!
If every 10 billion people can make a new earth every year, I think we should be able to get on top of this.
Line goes up. Can’t refute that!
Plot twist: the bio-dad is actually either Galactus or Ego.
7.5 trillion pound coins is a lot, I wonder how much they weigh.
Math checks out.
TWICE!
Mafs by mafks
-
How is size (“big”) even associated with mass (“weight”) in this relation?
-
What is a “pounds”?
They’re making the (possibly false) assumption that density will stay the same, so size must grow with weight.
Of course, it’s equally likely that size will remain constant. It changes or it doesn’t -> 50/50 odds. Until the point it all collapses into a black hole.
-